Google OR-Tools

Rohit

May 31, 2020

Today, I am going to introduce you to one of the amazing tools offered by google - Google OR-Tools. A great tool when it comes to optimizations under constraints. Google OR-Tools let you solve some complex optimization problems under great ease. If you have ever been stucked into a problem which requires you to find an optimal solutions to a given equation then you must check onto this amazing tool for yourself. Let’s get started.

Introduction

“OR-Tools is open source software for combinatorial optimization, which seeks to find the best solution to a problem out of a very large set of possible solutions.” - Google

Some of the examples provided by google include :-

Constraint Programming
Vehicle Routing
Linear or Mixed-Integer programming
Graph Algorithms

For now, i am only familier with Linear Programming. So, I am going to discuss this below.

Linear Programming

Linear Programming deals with the optimization (maximization or minimization) of linear functions subject to linear constraints. There are various methods used to solve a linear programming problem, mentioned below:-

Graphical method
Simplex method
M-method or method of penalties
Dual Simplex method.

All the listed above are in order of increasing complexity and each of them was an improvement over the other.
Here, Simplex method, devised in 1947 is the most used method but some problems have proved it to take exponential time. After this many researchers such as Leonid Khachiyan in 1947(weakly polynomial alogorithm), Narendra karmarkar in 1984(interior point method) have decreased the time complexity of algorithms.

Note :- Interior point algorithms have proved efficient on very large linear programs.

Formulation of the problem

Before we begin with some hands-on to Google OR-Tools let’s formulate a problem and understand some terminologies first.

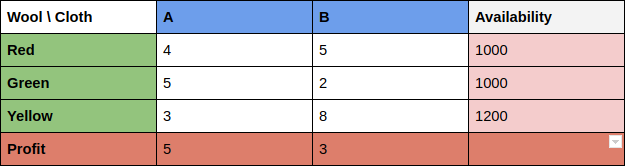
A company manufacturers two types of cloth, using three different colours of wool. 
One yard length of type A cloth requires:-
4 oz of red wool, 
5 oz of green wool and 
3 oz of yellow wool. 
One yard length of type B cloth requires:-
5 oz of red wool,
2 oz of green wool and 
8 oz of yellow wool. 
The wool available for manufacturer is:-
1000 oz of red wool,
1000 oz of green wool and 
1200 oz of yellow wool. 
The manufacturer can earn a profit of:-
$5 on one yard of type A cloth and
$3 on one yard of type B cloth. 
Find the best combination of quantites of:-
type A and type B cloth which gives him maximum profit
by solving the Linear programming problem.

Seems a tough one, but it will look less complex if we look at the problem like:-

Now let’s formulate in terms of some equations :-

Here the motive of manufacturer is to obtain the quantities of cloth A and cloth B. So, let the quantities of cloth A and cloth B be A and B which are also called the decision variables for the problem.
We have some requirements of materials for each type of cloth which inturn are bounded by the availabilty of that material. So, Next we shall define our constraints :-
```
4A + 5B <= 1000
5A + 2B <= 1000
3A + 8B <= 1200
```
Additionaly, a L.P.P problem must have non negative decision variables.
```
A, B >= 0
```
Lastly, manufacturer wants to maximize profit. Therefore, we need to define a objective function(Z) :-
```
Z = 5A + 3B
```

The Glop Linear Solver

The primary OR-Tools linear optimization solver is Glop, Google’s linear programming system. It’s fast, memory efficient, and numerically stable. The next section shows how to use Glop to solve a simple linear problem in all of the supported languages. - Google

Installation

For the reference to installation, it is best to follow the guidelines mentioned at here

Code

from __future__ import print_function
from ortools.linear_solver import pywraplp

def LinearProgrammingSolver():
  # instantiate the solver with name LinearProgrammingSolver
  solver = pywraplp.Solver('LinearProgrammingSolver',
                                pywraplp.Solver.GLOP_LINEAR_PROGRAMMING)
  # define your decision variables
  A = solver.NumVar(0, solver.infinity(), 'A')
  B = solver.NumVar(0, solver.infinity(), 'B')

  # Define first constraint for :- 4A + 5B <= 1000
  constraint0 = solver.Constraint(-solver.infinity(), 1000)
  constraint0.SetCoefficient(A, 4)
  constraint0.SetCoefficient(B, 5)
 
  # Define second constraint for :- 5A + 2B <= 1000
  constraint1 = solver.Constraint(-solver.infinity(), 1000)
  constraint1.SetCoefficient(A, 5)
  constraint1.SetCoefficient(B, 2)

  # Define third constraint for :- 3A + 8B <= 1200
  constraint2 = solver.Constraint(-solver.infinity(), 1200)
  constraint2.SetCoefficient(A, 3)
  constraint2.SetCoefficient(B, 8)

  # Define your objective function :- Z = 5A + 3B
  objective = solver.Objective()
  objective.SetCoefficient(A, 5)
  objective.SetCoefficient(B, 3)
  objective.SetMaximization()

  # Call the Solve() method for a solution
  solver.Solve()
  # Calculate the optimal solution
  opt_solution = 5 * A.solution_value() + 3 * B.solution_value()

  print('Number of variables =', solver.NumVariables())
  print('Number of constraints =', solver.NumConstraints())
  # The value of each variable in the solution.
  print('Solution:')
  print('x = ', A.solution_value())
  print('y = ', B.solution_value())
  # The objective value of the solution.
  print('Optimal objective value =', opt_solution)

# Driver Function call 
LinearProgrammingSolver()

Output

Number of variables = 2
Number of constraints = 3
Solution:
x =  176.47058823529403
y =  58.82352941176477
Optimal objective value = 1058.8235294117644

For code you can refer to my colab notebook on github

I hope you understood how a linear programming problem is formulated and solved with this amazing tool provided by google. For more info you can always refer to documentation and tutorials by google.

Note :- The above example was taken from one of my favourite book named :- Higher Engineering Mathematics by Dr. B.S. Grewal.

Conclusion

Today, we learnt how to formulate a linear programming problem and solve it using Google OR-Tools. Thanks for a reading. I’ll be continuing on more problems that are solved by Google OR-Tools. So, if you are interested see you around. Bye!